什么是生日悖论

生日悖论（Birthday paradox）是指假设一个班级有50个人，如果说在这个班级里概率大到可以肯定的说至少有2个人的生日相同（当然这里还不包括双胞胎，不包括闰年2月29日的情况），你信吗？

一般情况下，我们的直觉会认为班级里至少有两个人生日相同的概率会比较低，毕竟每个人的生日有365种选择，而班级只有50人，但是实际上计算得到在50个人的班级里出现同生日的概率甚至达到了惊人的97%！

正是因为理性的计算与日常的直觉经验产生了如此明显的矛盾，该问题才被称为生日悖论。

生日的概率计算

我们选择要用理性的方式来计算生日相同的概率是多少，但是对于计算有多少人生日相同，这个理解起来可能有点复杂和一时摸不着头脑。其实可以逆向思考下，反过来计算下50个人的班级里每个人生日不在同一天的概率是多少，再用总概率1减去生日不同的概率，最后不就能得到该班级找那个生日相同的人的概率是多少了吗。

先随便抽了1位同学，他的生日肯定可以是365天的任意一天，那么用数字计算表示就是：$\frac{365}{365}$，因为他有365中可能性。

注意：或许，很多人会认为应该是$\frac{1}{365}$，理由是每个人的生日只占一年中的一天。这里要理清一点，我们不是求每位同学日期的占比率，如果是占比率那任何一个人的生日都只可能是$\frac{1}{365}$。我们需要计算的是第一位同学的生日在一年中有多少种可选性，这是在你不知道的情况下计算的，所以第一位同学的生日可以有365种可能，（事件可能数量 / 总事件数）所以就是$\frac{365}{365}$。

接下来再抽第2位同学，因为要计算的是每个人生日不同的概率，那么前一位同学无论他的生日日期最终是哪一天，肯定会占用365天中的一个日期名额。所以第2位同学的生日可选择的数量只剩下364种了，就是$\frac{364}{365}$。而第3位同学就是$\frac{363}{365}$，以此类推到第50位同学时可选择的范围前面已占用49个名额，剩下就是$\frac{365-49}{365}=\frac{316}{365}$。

由于每个人都是随机独立事件，所以我们将该班级每个人的生日可能概率想乘，得到的即是全班50个人生日各自不同情况下的概率。

$\hat{p}$为假设班级里50位同学各自生日都不同的概率：$\hat{p}=\frac{365}{365}\times\frac{364}{365}\times\frac{363}{365}...\times\frac{316}{365}$

$p$为我们最终想知道的至少两人生日相同的概率，既然前面已经求得所有人生日不同的概率$\hat{p}$，那么拿总数1减一下就可以得出至少有两人生日相同的概率：$p=1-\hat{p}=1-\frac{365}{365}\times\frac{364}{365}\times\frac{363}{365}...\times\frac{316}{365}$

现在，计算包含 n 位同学时至少有两人生日相同的概率$p$为多少，转换成通用公式如下：

$\hat{p}=\frac{365\times364\times363...\times(365-n+1)}{365^{n}}=∏\limits_{i=1}^{n}\frac{365-i+1}{365}$

$p=1-\hat{p} = 1-∏\limits_{i=1}^{n}\frac{365-i+1}{365}$

同生日的概率分布可视化

总结出通用公式后就可以计算在出基于不同人数时至少两人生日相同的概率。

我用Python可视化了不同人数时的概率分布情况，你可以很直观的看到下图中红色横向的虚线是50%概率的位置，当x轴人数达到23左右的时对应的y轴概率基本已经在50%，也就是有50%的情况会出现至少有两个人生日相同，而当人数在60左右的时候蓝色曲线几乎水平并可以说接近100%了。

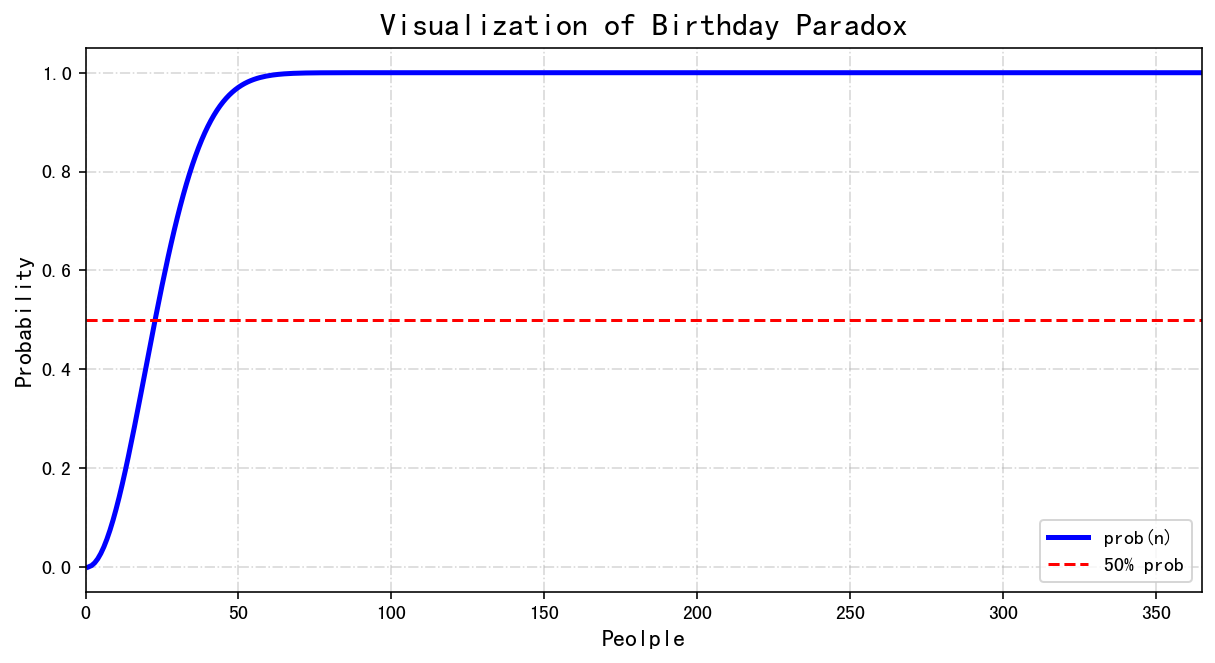
实现代码如下：

import math  
import matplotlib.pyplot as plt 

def birthday_paradox(size):  
    if size > 0:
        x_size = [i+1 for i in range(size)]
        y_prob = []
        log_x = 0

        for i in range(size):
            # 考虑到乘积数字太大，使用log的方式求解。
            # log(a)N = x 表示以a=10为底，真数N为365/365..365-i/365求值，该得的值为指数最后被使用。
            log_N = (365-i)/365
            log_x += math.log(log_N,10)
            p_hat = 10 ** log_x
            p = 1 - p_hat
            y_prob.append(p)

    plt.figure(figsize=(10,5))
    plt.plot(x_size, y_prob, linewidth=2.5, label='prob(n)', color='blue')

    # 设置水平线
    plt.axhline(0.5, linestyle='--', color='red', label='50% prob')
    # 绘制图例
    plt.legend()
    # 设置x轴范围
    plt.xlim(0, size)
    # 设置网格线型
    plt.grid(linestyle='-.', alpha=0.5)
    # 设置窗口标题
    plt.title('Visualization of Birthday Paradox', fontsize=16);
    # 设置坐标轴标签
    plt.xlabel('Peolple', fontsize=12)
    plt.ylabel('Probability', fontsize=12)


birthday_paradox(365)  

模式验证

通过之前对生日悖论的概率计算及可视化，我们明确知道了在不同人数群体时获得至少两个人生日相同的概率分布情况。但是如果实际真的出现指定数量的人数时，是否真的能接近我们计算的概率呢？

我做了一个模拟实验，实验的构思大致为先生成一年365天真实的日期范围（不用在意年份），测试人数为1至100人。因为我们要观察不同人数群体生日相同的概率，所以也就会出现100个群体样本。如，第1个样本只有1人，第2个样本有2人，以此类推，第100个样本就包含100个人。而每个样本的人群都会随机分配生日日期，接着针对这100个样本再分别做1次，10次，100次，1000次的实验，观察生日是否出现相同的实验。直到每个群体的反复实验完成后，用 相同生日的累积次数 / 总的循环实验次数 就可以获得每个特定人群出现生日相同的概率值。理论上来说，每个人群数量得出的实验概率值会与生日悖论的概率相同，那么两条概率曲线应当是吻合的。

如下是可视化的结果，可以发现只做1次实验的时候，1至50人时的紫色概率曲线波动十分明显，结果不是0.0就是1.0（100%）。回忆起之前在生日悖论概率计算时，当群体达到20人时存在两人生日相同的概率应当在0.41左右，但我们的实验结果却是1.0。这其实很好解释，正因为概率低所以实验的次数越少实验结果才越不稳定，只执行1次实验的话结果可想而知，要么存在要么不存在，类似于一个阶跃函数。要知道我们得到的生日悖论概率其实是一个期望概率，只有经过多次实验也就是根据大数定律才会趋向于最终概率值。可以看到当我们运行的次数越来越多直到1000次的时候，紫色的实验概率曲线最终与蓝色曲线基本吻合在一起，如果继续增加实验次数肯定会重叠，也就说明模式验证的概率是符合的。注：另外要说明的是，模拟测试的生日概率是平均分布的（现实生活中，出生机率不是平均分布的）。

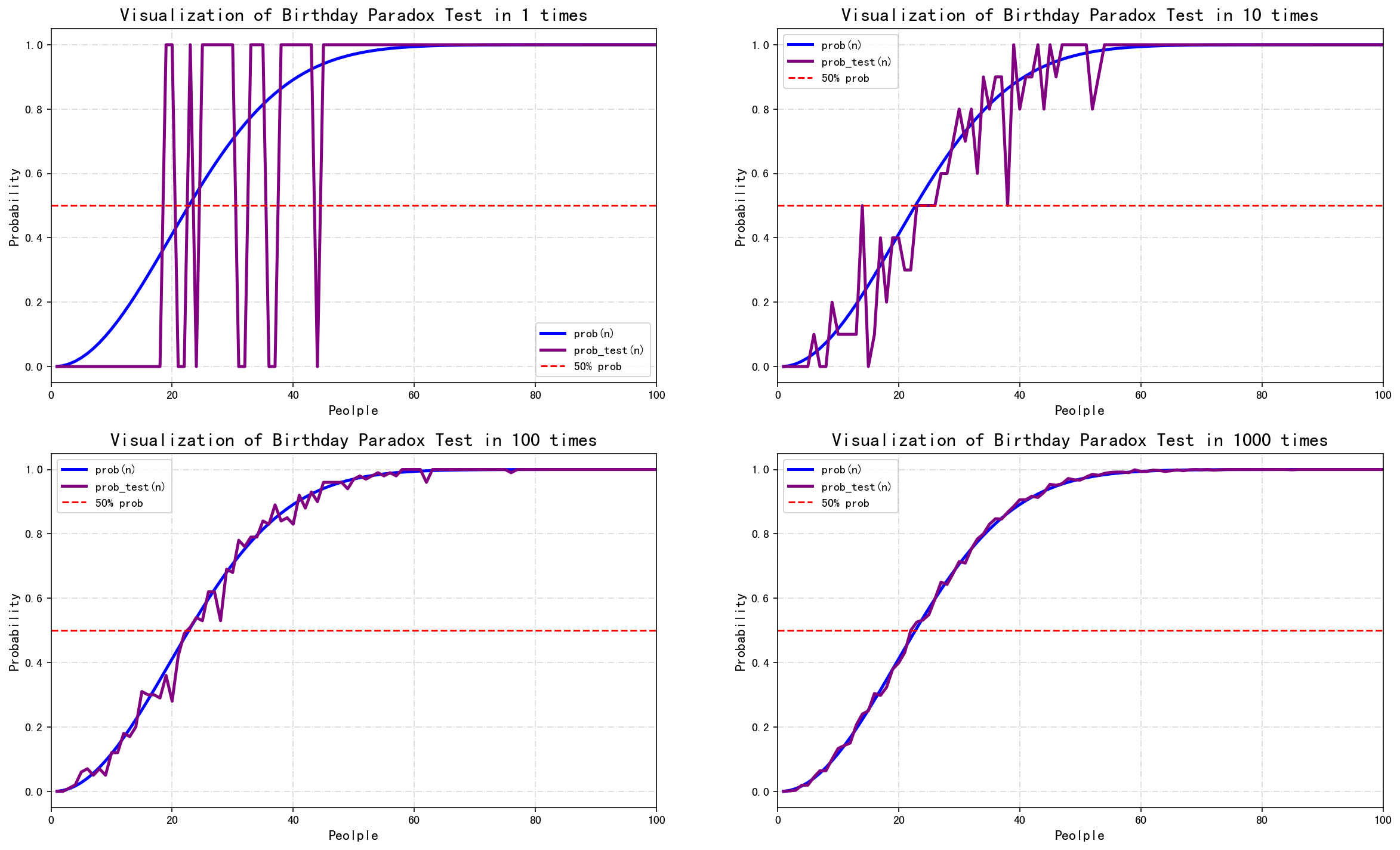
代码部分如下：

import pandas as pd  
import numpy as np  
import datetime  
import time  
from collections import Counter

# 验证生日悖论概率
x = []  
y = []  
date_range = pd.date_range('2019/1/1', periods=365).strftime("%Y-%m-%d").to_list()  
def birth_paradox_test(size, times):  
    global x
    global y
    x = [s+1 for s in range(size)]

    for i in range(1, size+1):
        same_date_sum = 0
        for _ in range(times):
            value = Counter(np.random.choice(date_range, size=i, replace=True)).most_common(1)[0][1]
            if value > 1:
                same_date_sum += 1
        prob = same_date_sum/times
        y.append(prob)


# 生日悖论概率分布        
x_size = []  
y_prob = []  
def birthday_paradox(size):  
    global x_size
    global y_prob
    if size > 0:
        x_size = [i+1 for i in range(size)]
        y_prob = []
        log_x = 0

        for i in range(size):
            # 考虑到乘积数字太大，使用log的方式求解。
            # log(a)N = x 表示以a=10为底，真数N为365/365..365-i/365求值，该得的值为指数最后被使用。
            log_N = (365-i)/365
            log_x += math.log(log_N,10)
            p_hat = 10 ** log_x
            p = 1 - p_hat
            y_prob.append(p)



plt.figure(figsize=(20,12))  
# 循环4次，每次以1, 10, 100, 1000循环次数。
times_list = [1, 10, 100, 1000]  
map_no = 1  
# 设置人数最大为100人
size = 100

for time in times_list:  
    birthday_paradox(size)
    birth_paradox_test(size, times=time)

    plt.subplot(2,2, map_no)
    map_no += 1

    plt.plot(x_size, y_prob, linewidth=2.5, label='prob(n)', color='blue')
    plt.plot(x, y, linewidth=2.5, label='prob_test(n)', color='purple')

    # 设置水平线
    plt.axhline(0.5, linestyle='--', color='red', label='50% prob')
    plt.legend()
    plt.xlim(0, size)
    plt.grid(linestyle='-.', alpha=0.5)
    plt.title(f'Visualization of Birthday Paradox Test in {time} times', fontsize=16);
    plt.xlabel('Peolple', fontsize=12)
    plt.ylabel('Probability', fontsize=12)

    x = [] 
    y = []
    x_size = [] 
    y_prob = []

扩展思考

既然我们已经通过理性的计算和了解了一个班级存在至少两个人生日相同的概率如此之高，但是你有没有发觉，回想自己的学生生涯，在自己经历各个年级阶段时，却很少发现自己与班级里的同学生日相同，这是为什么呢？似乎又产生矛盾了。这其实也可以通过理性计算来解惑。

要计算与我（或者说特定某个人）的生日相同的概率是多少，我们依然使用之前的逆向思维来思考，可以计算与我生日不同的人的概率有多少，最后相减一下就可以得出有多少概率可以使生日相同。

假设还是在50个人的班级里，首先我的生日（也可以说特定某个人的生日）可以是一年中的任意一天（实际情况肯定知道自己的生日是哪一天，但是从理性计算角度而言可以允许是一年里的任一天），那么我自己的生日可以有365种可能性，概率就是$\frac{365}{365}$。别忘了，现在计算的是生日不相同的概率，所以第二个人的生日不能与我的生日相同，那么他的生日只能有364种可选性，概率就是$\frac{364}{365}$。重点来了，第三个人他的生日依然有364种可能，为什么呢？因为生日的日期参照值是我的生日，只要与我生日的日期不同，哪怕第三个人和别人生日存在相同都没关系，所以依然还有364种可选性，那么概率依然是$\frac{364}{365}$，以此类推，直到班级里第50个人，他与我的生日不同的概率依然是$\frac{364}{365}$。

所以在50个人的班级里与我生日不同的概率计算如下：

$\hat{p}=\frac{365}{365}\times\frac{364}{365}\times\frac{364}{365}...\times\frac{364}{365} = 1\times\frac{364}{365}\times\frac{364}{365}...\times\frac{364}{365}$

我们转换成通用公式如下：

$\hat{p} = 1\times(\frac{364}{365})^{n-1}$

最后用总数1减去$\hat{p}$就可以得到和我的生日相同的概率：$p = 1-\hat{p}=1-1\times(\frac{364}{365})^{n-1}$。

老样子，我们同样用可视化描绘出不同人数时与自己生日相同的概率分布情况。

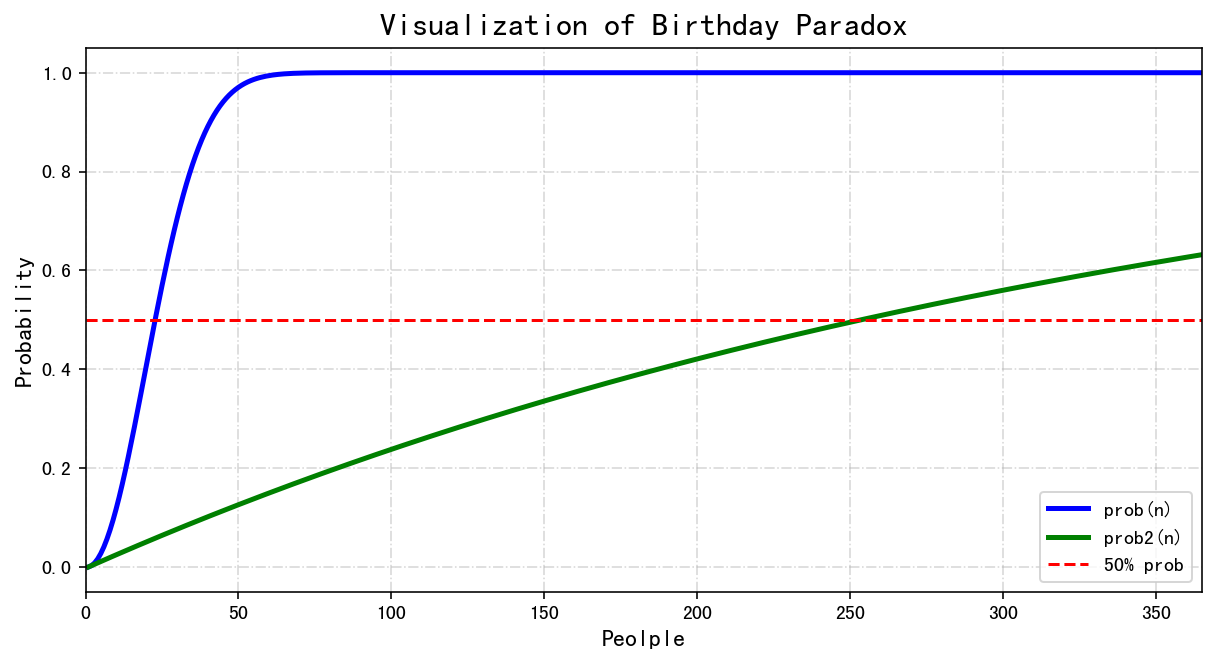
我们可以发现，大概到250人的时候，才有50%的几率会有至少1个人与我的生日相同。所以如果我们仅仅关注的是一群人里有至少两个人的生日相同，那只需要满足有23个人时就可以达到50%，而如果以自己或者某一个人的生日为参照中心的时候这个人数的要求就很高了。

实现代码如下：

import math  
import matplotlib.pyplot as plt 

def birthday_paradox(size):  
    if size > 0:
        x_size = [i+1 for i in range(size)]
        y_prob = []
        y_prob_2 = []
        log_x = 0

        # 便于理解，统一序号以1开始，range(1, n)只显示1,2,3..n-1。所以最终
        for i in range(size):
            # 考虑到乘积数字太大，使用log的方式求解。
            # log(a)N = x 表示以a=10为底，真数N为365/365..365-i/365求值，该得的值为指数最后被使用。
            # 注：因为这里i是从0开始，所以直接365-i即可，不需要365-i+1。
            log_N = (365-i)/365
            log_x += math.log(log_N,10)
            p_hat = 10 ** log_x
            p = 1 - p_hat
            y_prob.append(p)

            # 注：需要循环累积乘以n-1次，因为这里i是从0开始，所以不需要i-1。
            p_hat_2 = 1* math.pow(364/365, i)
            p_2 = 1 - p_hat_2
            y_prob_2.append(p_2) 

    plt.figure(figsize=(10,5))
    plt.plot(x_size, y_prob, linewidth=2.5, label='prob(n)', color='blue')
    plt.plot(x_size, y_prob_2, linewidth=2.5, label='prob2(n)', color='green')

    # 设置水平线
    plt.axhline(0.5, linestyle='--', color='red', label='50% prob')
    # 绘制图例
    plt.legend()
    # 设置x轴范围
    plt.xlim(0, size)
    # 设置网格线型
    plt.grid(linestyle='-.', alpha=0.5)
    # 设置窗口标题
    plt.title('Visualization of Birthday Paradox', fontsize=16);
    # 设置坐标轴标签
    plt.xlabel('Peolple', fontsize=12)
    plt.ylabel('Probability', fontsize=12)


birthday_paradox(365)  

所以，综合上述来说，我们的潜在直觉并没有错，错的是我们没有从正确的角度去理解问题。因此，当我们拨开直觉的谎言去理解问题，才会觉得如此不可以思议。