帕累托分析法是基于帕累托法则的一种分析法。

先来说说什么是帕累托法则，其原型是19世纪意大利经济学家帕累托所创的库存理论。帕累托运用大量的统计资料分析当时的一些社会现象，概括出一种关键的少数和次要的多数的理论，并根据统计数字画成排列图，后人把它称为帕累托曲线图。简单的说，帕累托法则其实就是我们常说的二八法则，在经济学定律中说的是80%的财富掌握在20%的人手中，而在运营中说的则是80%的贡献度来自于20%的用户。

而基于帕累托法则的帕累托分析法（Pareto Analysis）是制定决策的统计方法，用于从众多任务中选择有限数量的任务以取得显著的整体效果。

下图是我基于Pandas随机模拟出的一组产品数据，并结合Matplotlib来展现这组数据的相关帕累托曲线图。

如图可见，蓝色的条形柱状图代表了每款产品的销售金额，每一个橘色百分点标记代表了从左往右的销售累计占比。其中红色的垂直虚线则是一条数据占>=80%的分界线，也就代表了这条分界线之前的7款产品（即，'G7', 'MX3', 'R9Plus' , 'A37', 'Note5', 'X5Pro', 'A50'）占到了总销售额中83.91%的销售份额，之后其余的3款产品占比只有16.09%。假如放到现实场景中，就可以根据市场情况制定某些决策，如是否要撤销某些产品的研发。

接下来为了更好的理解代码是如何实现的，我将分解代码成若干段来说说明。首先我用Pandas模拟10组虚拟产品数据。

import numpy as np  
import pandas as pd  
import matplotlib.pyplot as plt

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

# 创建模拟数据，10个品类产品的销售额     
data = pd.Series(np.random.randn(10)*500+1000,  
                 index=['A37','A50','R7S','Note5',
                        'G7','R9_Plus','5C','X5_Pro',
                        'MX3','M5'])
print(data)  

通过输出data变量值查看如下，左侧的index是我们虚拟的10组产品名称，而右侧对应的数值则是通过random.randn随机产生的10组基于标准正态分布的伪数据。

A37        1784.729567  
A50         198.971079  
R7S         985.258417  
Note5      1348.619119  
G7         1330.237773  
R9_Plus     188.307306  
5C         2105.157302  
X5_Pro     1225.447782  
MX3         957.038300  
M5         1346.797999  
dtype: float64  

接着，我们将所有的数据从大到小降序排列并以此构建柱状图。

其中要注意的一点是，为什么需要降序排列呢？因为考虑到我们要制作的是累计占比，同样是计算累计相加值满足>=80%，从小到大升序排列 与 从大到小降序排列 相比 降序排列能以更少的数据个数预先满足累计相加值>=80%，也就能体现帕累托法则的二八法则，少数掌握多数的原理。

# 将数值按照从大到小排序
data.sort_values(ascending=False, inplace=True)  
# 构建画布
plt.figure(figsize=(10,6))

# 先构建一个从大到小排列的，标准柱状图。
data.plot(kind='bar', colormap='GnBu_r', width=0.6, edgecolor='black', rot=0)

plt.xlim(-1,11)  
plt.ylim(0,2000)

plt.xlabel('产品名')  
plt.ylabel('销售金额')  
plt.title('销售情况')  
plt.legend(['销售金额'], loc='upper right')  

输出图如下：

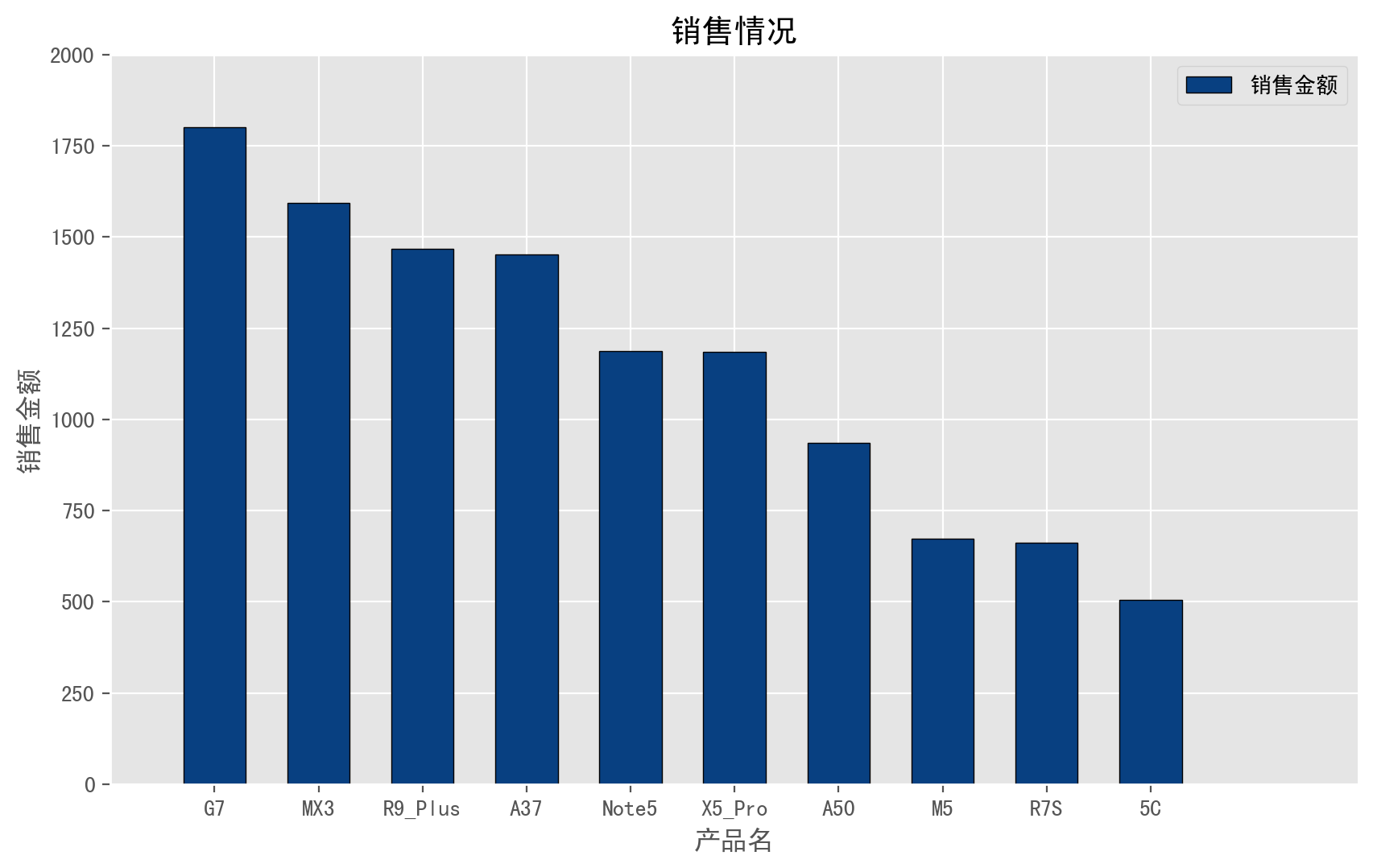
之后，需要绘制另一条累计占比的百分比图。首先需要通过cumsum函数得到每个产品时的当前累计值，并用这个累计值去除以总销售金额得到的就是该产品当前的累计占比的百分比数值。得到每个产品当前的累计占比的百分比数值后就可以通过布尔索引筛选出>=80%的产品名称。有了这个产品名称就可以获得该产品的索引位置编号，而这个索引位置十分重要，因为这有助于我们之后用来标注那条红色分界线的具体位置。

# 累加值 除以 总数值 得到每个阶段累加值的占比值。
proportion = data.cumsum() / data.sum()

# 用布尔索引列出大于等于0.8的数值列表，而列表里第一行就是大于80%的关键点，我们取得它的索引名称。
key = proportion[proportion >= 0.8].index[0]

# 根据之前得到的索引名称，就可以从data数据中得到该名称的索引位置。
key_number = data.index.tolist().index(key)

proportion.plot(style='--ko', secondary_y=True, color='#FFA500')

plt.axvline(key_number, linestyle='--', color='red')

for x, y, s in zip(range(len(data)), proportion.values, proportion):  
    if x == key_number:
        plt.text(key_num+0.2, y-0.035, '累计占比为 {:.2%}'.format(s), color='red', fontsize=12)
    else:
        plt.text(x+0.3, y-0.035, "{:.2%}".format(s), fontsize=12, horizontalalignment='center', color='black')

plt.ylabel('销售（比例）')  
plt.legend(['累积占比'], loc='upper center')  

之后将两段代码合并，也就是两张图合并为一张图就形成了我们一开始提到的帕累托曲线图。

最后放上完整代码如下：

import numpy as np  
import pandas as pd  
import matplotlib.pyplot as plt

%matplotlib inline
%config InlineBackend.figure_format = 'retina'

# 创建模拟数据，10个品类产品的销售额     
data = pd.Series(np.random.randn(10)*500+1000,  
                 index=['A37','A50','R7S','Note5',
                        'G7','R9_Plus','5C','X5_Pro',
                        'MX3','M5'])


# 将数值按照从大到小排序
data.sort_values(ascending=False, inplace=True)  
# 构建画布
plt.figure(figsize=(10,6))

# 先构建一个从大到小排列的，标准柱状图。
data.plot(kind='bar', colormap='GnBu_r', width=0.6, edgecolor='black', rot=0)  
plt.xlim(-1,11)  
plt.ylim(0,2000)  
plt.xlabel('产品名')  
plt.ylabel('销售金额')  
plt.title('销售情况')  
plt.legend(['销售金额'], loc='upper right')

# 累加值 除以 总数值 得到每个阶段累加值的占比值。
proportion = data.cumsum() / data.sum()

# 用布尔索引列出大于等于0.8的数值列表，而列表里第一行就是大于80%的关键点，我们取得它的索引名称。
key = proportion[proportion >= 0.8].index[0]

# 根据之前得到的索引名称，就可以从data数据中得到该名称的索引位置。
key_number = data.index.tolist().index(key)

proportion.plot(style='--ko', secondary_y=True, color='#FFA500')

plt.axvline(key_number, linestyle='--', color='red')

for x, y, s in zip(range(len(data)), proportion.values, proportion):  
    if x == key_number:
        plt.text(key_num+0.2, y-0.035, '累计占比为 {:.2%}'.format(s), color='red', fontsize=12)
    else:
        plt.text(x+0.3, y-0.035, "{:.2%}".format(s), fontsize=12, horizontalalignment='center', color='black')

plt.ylabel('销售（比例）')  
plt.legend(['累积占比'], loc='upper center')  

总结

画帕累托图最重要的几点是要将数据从大到小排序，这主要是为了能体现帕累托法则的二八法则，少数掌握多数的原理。当数据以降序的方式排列后，计算每个列数据累计占比百分比数值。有了百分比数值，我们就可以将数据可视化，可视化后可以很清楚的从图中来区分哪些对应的产品满足了>=80%的贡献。