22 8月 2019 • 标签 Python, 技术博文, 数据分析

数据处理 - 异常值分析及可视化

异常值(Outlier) 是指样本中的个别值，其数值明显偏离所属样本的其余观测值。大多数情况下，异常值是由于数据录入或者数据后台数据运算错误导致。但是要说明的一点，异常值只是代表这个值属于异常而不一定代表这个值就是错误的。所以对于异常值的处理要适具体情况而定。

检测到了异常值，我们需要对其进行一定的处理。而一般异常值的处理方法可大致分为以下几种：

直接将含有异常值的记录删除。
视为缺失值：将异常值视为缺失值，利用缺失值处理的方法进行处理。
平均值修正：可用前后两个观测值的平均值修正该异常值。
不处理：直接在具有异常值的数据集上进行数据挖掘。

具体如何处理异常值我们不在这里涉及，而是主要讲如何检测异常值，检测的分析方法多种多样，一般异常值的检测方法有基于统计的方法，基于聚类的方法，以及一些专门检测异常值的方法等。异常值会大幅度地改变数据分析和统计建模的结果。

由于检测分析的方法有许多，这里主要使用两种检测异常值的方法分别为：3σ准则（又称为拉依达准则）与

箱型图 两种方式对异常值进行检测分析。

一、3σ准则

3σ准则又称为拉依达准则。所谓3σ，当数据被定义为在一组测定值中与平均值的 σ（标准偏差）超过3倍时，这个值就被认为是异常值，而这个异常值的概率通常小于0.3%，用公式可以理解为 $p(|x-\mu|>3 \sigma) \leqslant 0.003$ 。

也可以从如下的正态分布图中更好的理解（其中，$\mu$代表均值，$x=\mu$即为图像的对称轴），可以发现大部分数值都在 $(\mu-3σ，\mu+3σ)$ 范围内概率占到了99.73%，而超出这个范围区间的可能性仅占不到0.3%，这个区间范围内的数值就是异常值。

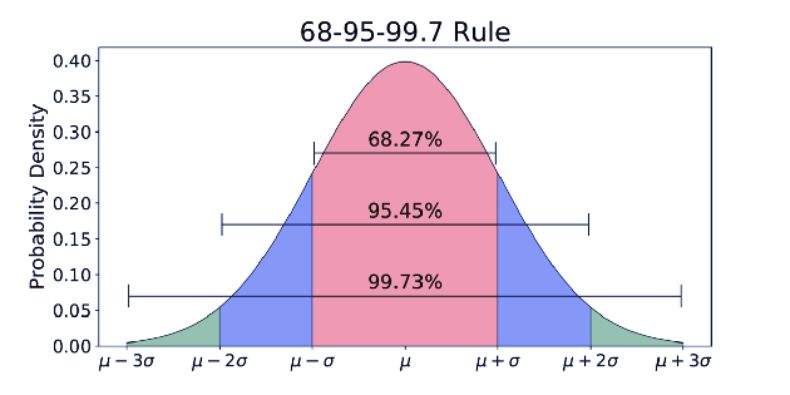
另外要注意的是，这种判别处理原理及方法仅局限于对正态或近似正态分布的样本数据处理，以及建议当数据量大的时候使用。

3σ准则可视化部分

接下来，看看如何用可视化的方式查看异常值。之前提到过使用3σ准则有个前提就是数据必须服从正太分布，所以为了便于实验，这里使用numpy.random.randn()函数随机产生基于正太分布的数据值。

第一张图使用了KDE画出密度曲线后，根据3倍标准偏差画出对应红色虚线位置，这个红色虚线以内的范围占99.73%，而以外的范围占不到0.3%（为异常值范围）。

第二张图使用了散点图的方式将所有数据值以数据点的方式画出来，其中蓝色点为正常值，4个红色点就是异常值。而判断异常值的方式就是我们之前提到的公式：$|x-\mu|>3 \sigma$

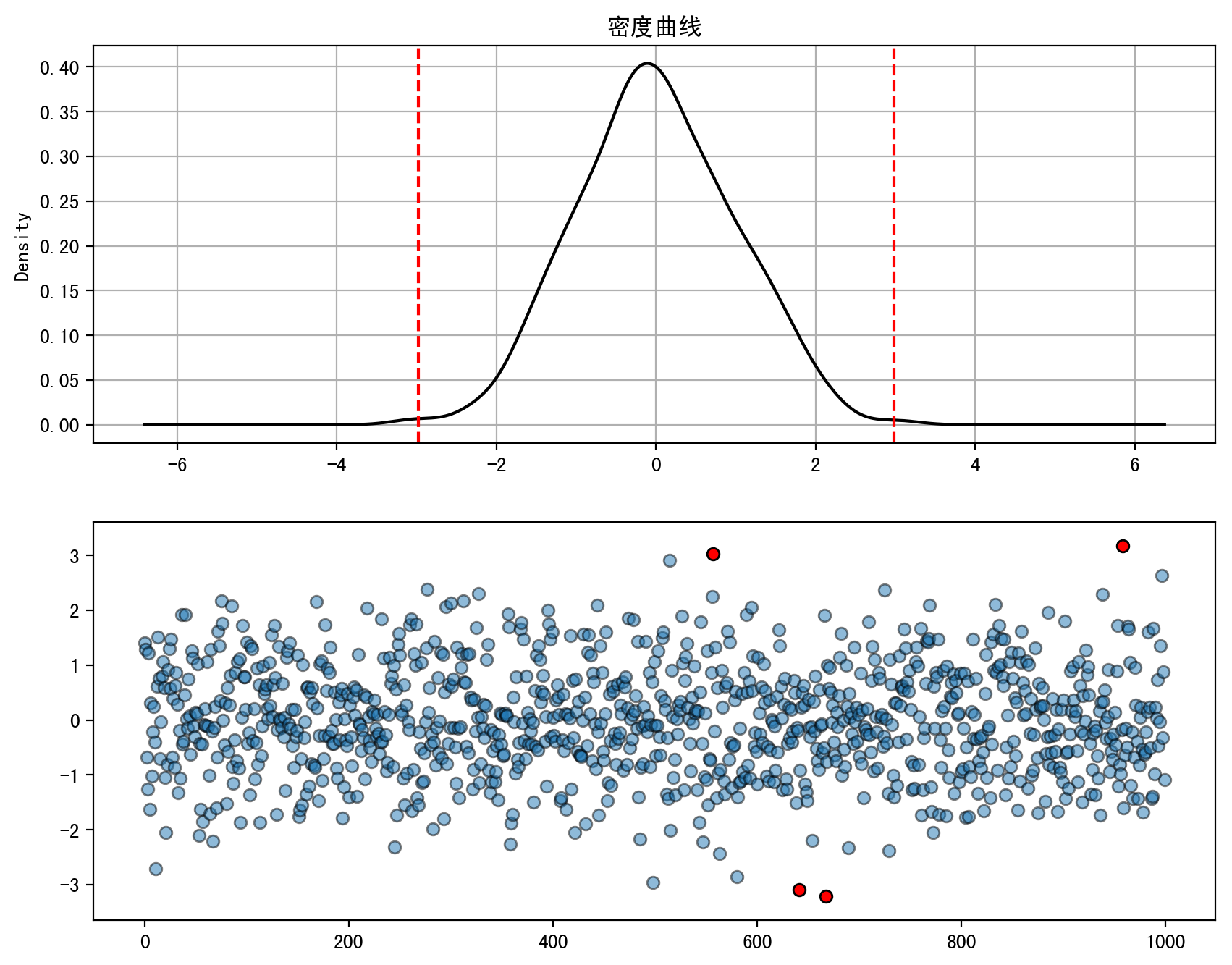
总结3σ准则的分析大致为如下几个步骤：

首先需要保证需要检验的数据列大致上服从正态分布。
然后计算需要检验的数据列的标准差。
最后比较数据列的每个值，是否大于标准差的3倍。
选择用可视化的方式呈现出来。

3σ准则代码实现

如下是代码的实现部分：

import numpy as np  
import matplotlib.pyplot as plt  
import pandas as pd  
from scipy import stats  
%matplotlib inline
%config InlineBackend.figure_format = 'retina'

# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']  
plt.rcParams['axes.unicode_minus'] = False

# 创建虚拟数据
data = pd.Series(np.random.randn(1000))  
data.head()


# 用K-S检测正态性
p = stats.kstest(data, 'norm', (mu, std))  
if p.pvalue > 0.05:  
    print(f'p值为 {p.pvalue}是正态分布')
else:  
    print(f'p值为 {p.pvalue}不是正态分布')

# 构建画布
fig = plt.figure(figsize=(10, 8))  
ax1 = fig.add_subplot(211)

### 绘制kde密度图 ###
data.plot(kind='kde', grid=True, style='-k', title='密度曲线')

std = data.std()  
plt.axvline(3*std, color='red', linestyle='--')  
plt.axvline(-3*std, color='red', linestyle='--')



### 绘制散点图 ###
mu = data.mean()  
# 筛选出异常值|x-u|>3σ
outlier = data[np.abs(data - mu) > 3*std]

# 筛选出正常值
data_correct = data[np.abs(data - mu) <= 3*std]

ax2 = fig.add_subplot(212)  
ax2.scatter(data_correct.index, data_correct.values, edgecolor = 'black', alpha = 0.5)  
ax2.scatter(outlier.index, outlier.values, color = 'red', edgecolor = 'black')

二、箱型图

有些数据不一定符合正太分布，如果用几倍的σ去检测异常值就不合适，那么我们如何来判断这些变化是否在合理的范围呢？可以考虑使用箱型图，箱型图的四分位距（IQR）对异常值进行检测，也叫Tukey's Test。我们可以看下如下箱型图的样式：

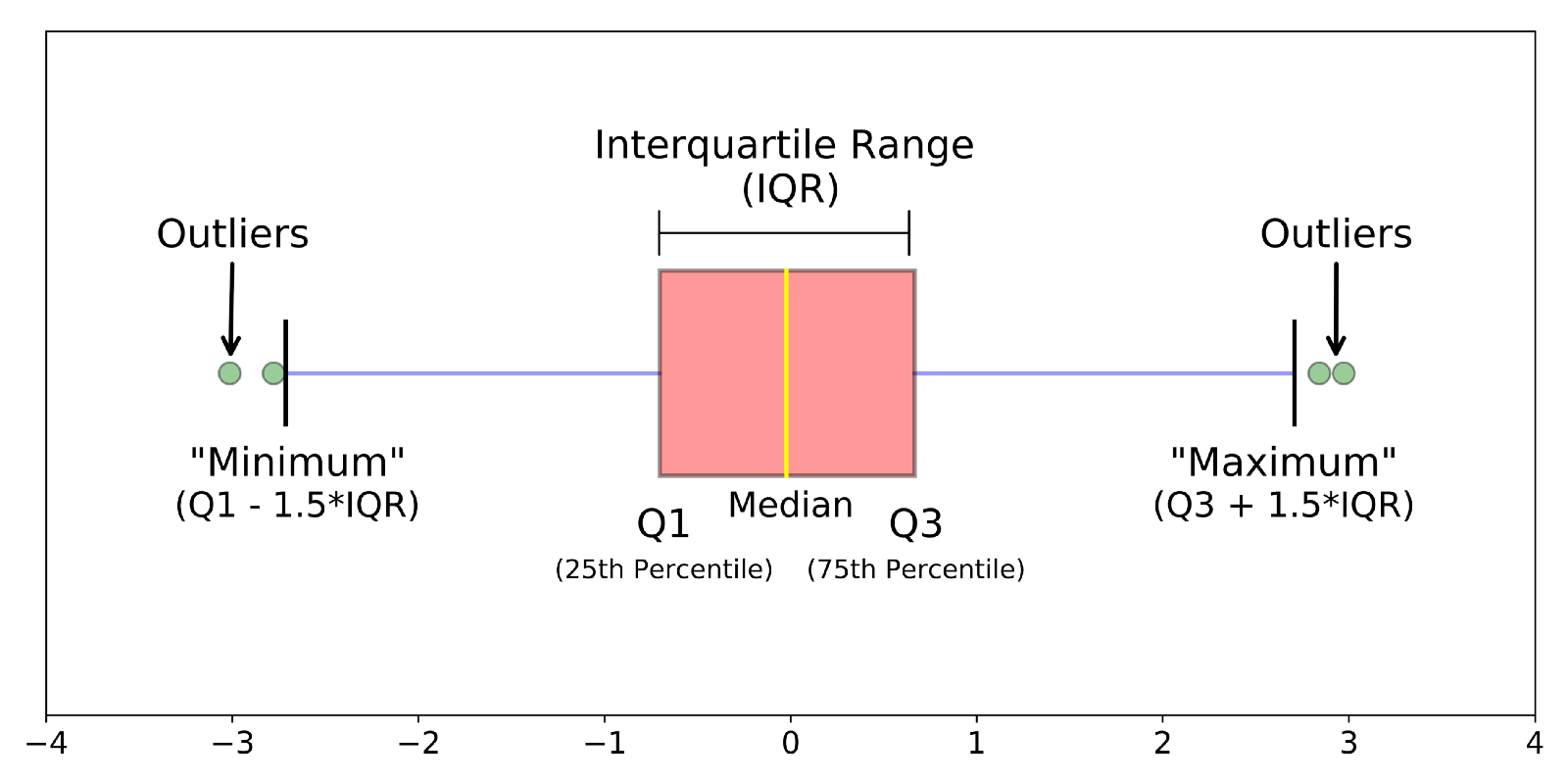
箱型图中间是一个箱体，也就是粉红色部分，箱体左边，中间，右边分别有一条线，左边是下四分位数（Q1），右边是上四分位数（Q3），中间是中位数（Median），上下四分位数之差是四分位距（称IQR）。IQR也可以说指的是两个四分值之间的范围大小。用 Q1-1.5*IQR 得到下边缘（最小值），Q3+1.5*IQR 得到上边缘（最大值），在上边缘之外的数据就是极大异常值，在下边缘之外的数据极小异常值，总之在上下边缘之外的数据就是异常值。另外要说明的是图中的数值 1.5 是一个可变的系数，表示的是中度异常；对于重度异常的情况，可以视情况而定将系数提高至 3。

箱型图可视化

如下是基于我用python模拟的数据并以（横向）箱型图的方式呈现的可视化结果，从下图中可以很清楚的发现，左侧也就是下边缘（最小值）外有5个红色的数据点，右侧也就是上边缘（最大值）外有3个红色的数据点，总计一共有8个异常值。

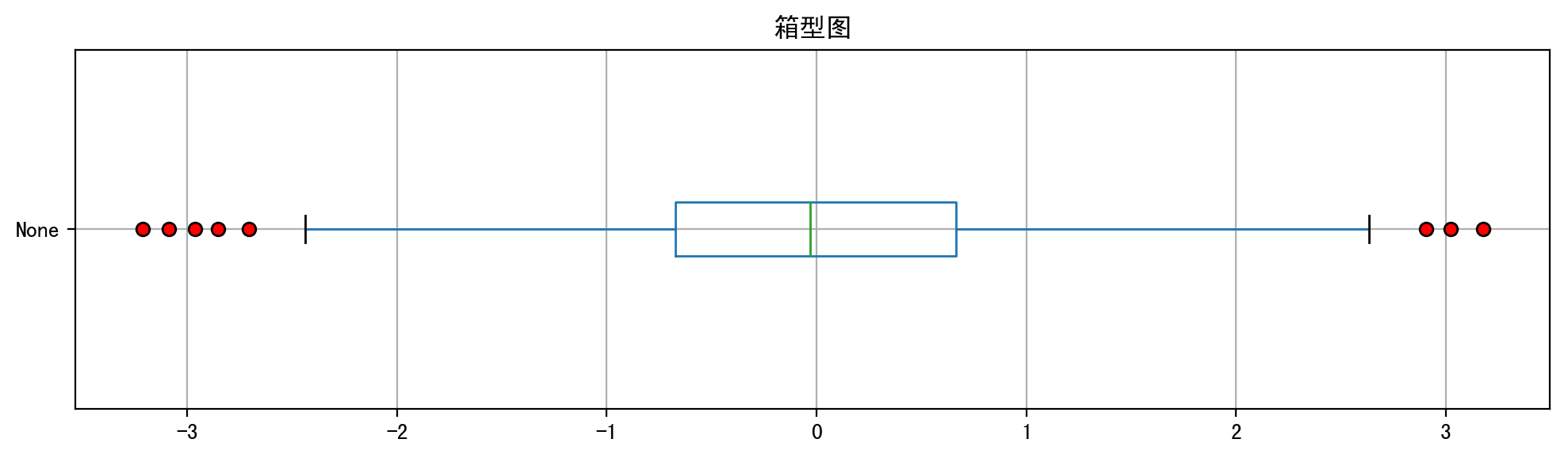
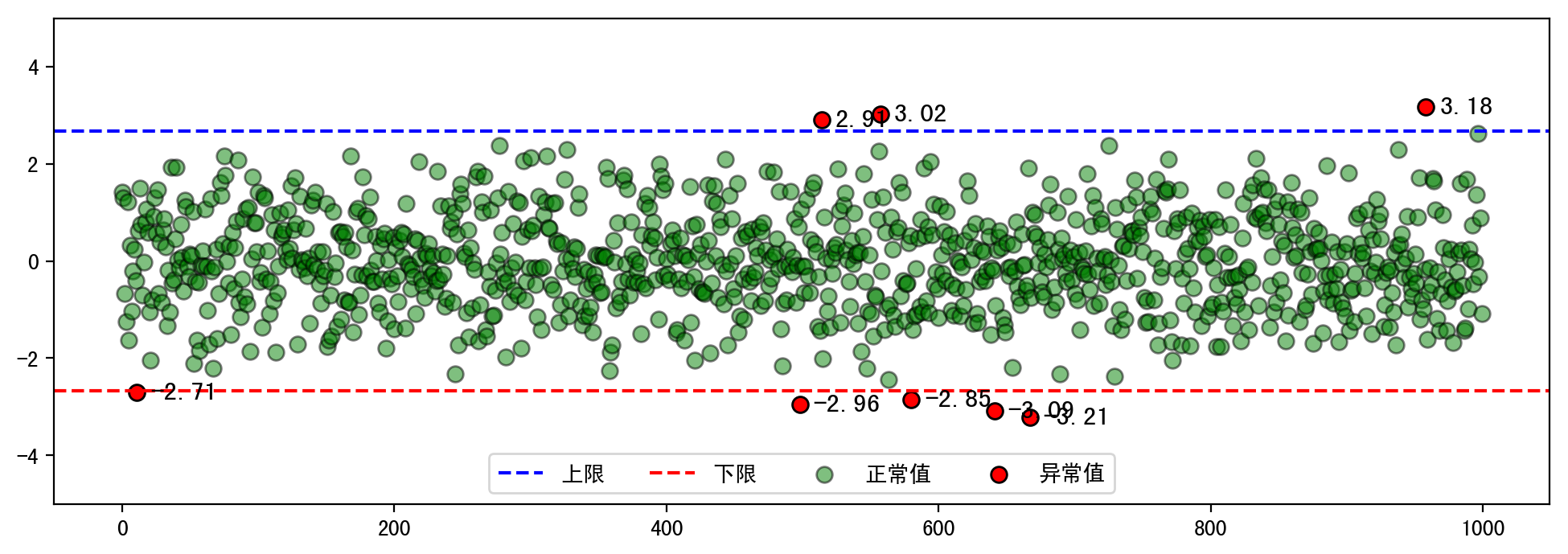
然后我又通过散点图的方式来可视化异常值的分布情况，如下我做了一些定制，为每个异常值标注数值信息。最终我们可以发现一共有个8个异常值，因为这8个异常值属于比最大值还要大，所以在上限上方，显然这与之前的箱型图出现的异常值数量相吻合。

箱型图代码实现

代码部分如下（其中data数据沿用最早的data模拟数据），或许你会问为什么同样的数据得出的异常值个数不同呢，通常来说通过箱型图的以分位数做判断的方式得到的异常值比标准偏差更精确细腻，所以异常值得到的更多。毕竟很少会有大于3倍标准偏差的数据，那么通过3σ准则分析得到的异常值自然就少的多。

### 构建一个箱型图 ###
fig = plt.figure(figsize = (12, 3))  
ax = fig.add_subplot(111)  
# vert = True 时 箱型图为垂直方式
red_circle = dict(markerfacecolor='r', marker='o')  
data.plot.box(vert = False, grid = True, ax = ax,  
              title='箱型图', flierprops=red_circle)



### 构建一个散点图 ###
# 通过describe()函数获得数据的统计量描述信息
data_des = data.describe()  
q1 = data_des['25%']  
q3 = data_des['75%']  
iqr = q3 - q1  
minimum = q1 - 1.5 * iqr  
maximum = q3 + 1.5 * iqr  
outlier = data[(data < minimum) | (data > maximum)]  
correct = data[(data >= minimum) | (data <= maximum)]

print('共有{}个异常值'.format(len(outlier)))

fig = plt.figure(figsize = (12, 4))

plt.scatter(correct.index, correct.values, s = 50,color = 'green', edgecolor = 'black', alpha = 0.5, label='正常值')  
plt.scatter(outlier.index, outlier.values, color = 'red', s = 50, edgecolor = 'black', label='异常值')

# 为异常值附上文字说明
for x, y in zip(outlier.index, outlier.values):  
    plt.text(x = x + 10, y = y - 0.15, s = '{:0.2f}'.format(y), color = 'black', fontsize = 12)

# 添加x横轴标线
plt.axhline(y = maximum, color = 'blue', linestyle = '--', label = '上限')  
plt.axhline(y = minimum, color = 'red', linestyle = '--', label = '下限')

plt.ylim(-5, 5)  
plt.legend(loc = 8, ncol = 4);

Anders Wang