1、什么是神经网络

神经网络是当前机器学习领域普遍所应用的，例如可利用神经网络进行图像识别、语音识别等，从而将其拓展应用于自动驾驶汽车等领域。神经网络的衍生变种目前有很多种，如CNN、RNN、GAN等，它们在不同应用场景有着各自针对性。但最简单且原汁原味的神经网络则是多层感知器（Muti－Layer Perception ，MLP）也叫人工神经网络(ANN,Artificial Neural Network)，除了输入输出层，它中间可以有多个隐层，最简单的MLP只含一个隐层，即三层的结构。只有理解经典的原版，才能更好的去理解功能更加强大的现代变种。

为了更好的理解，我画了手绘稿作为插图配合最后的代码来梳理人工神经网络的基本过程。

在理解神经网络前，不得不先引申出一点就是我们人类大脑中的基本单元———神经元。

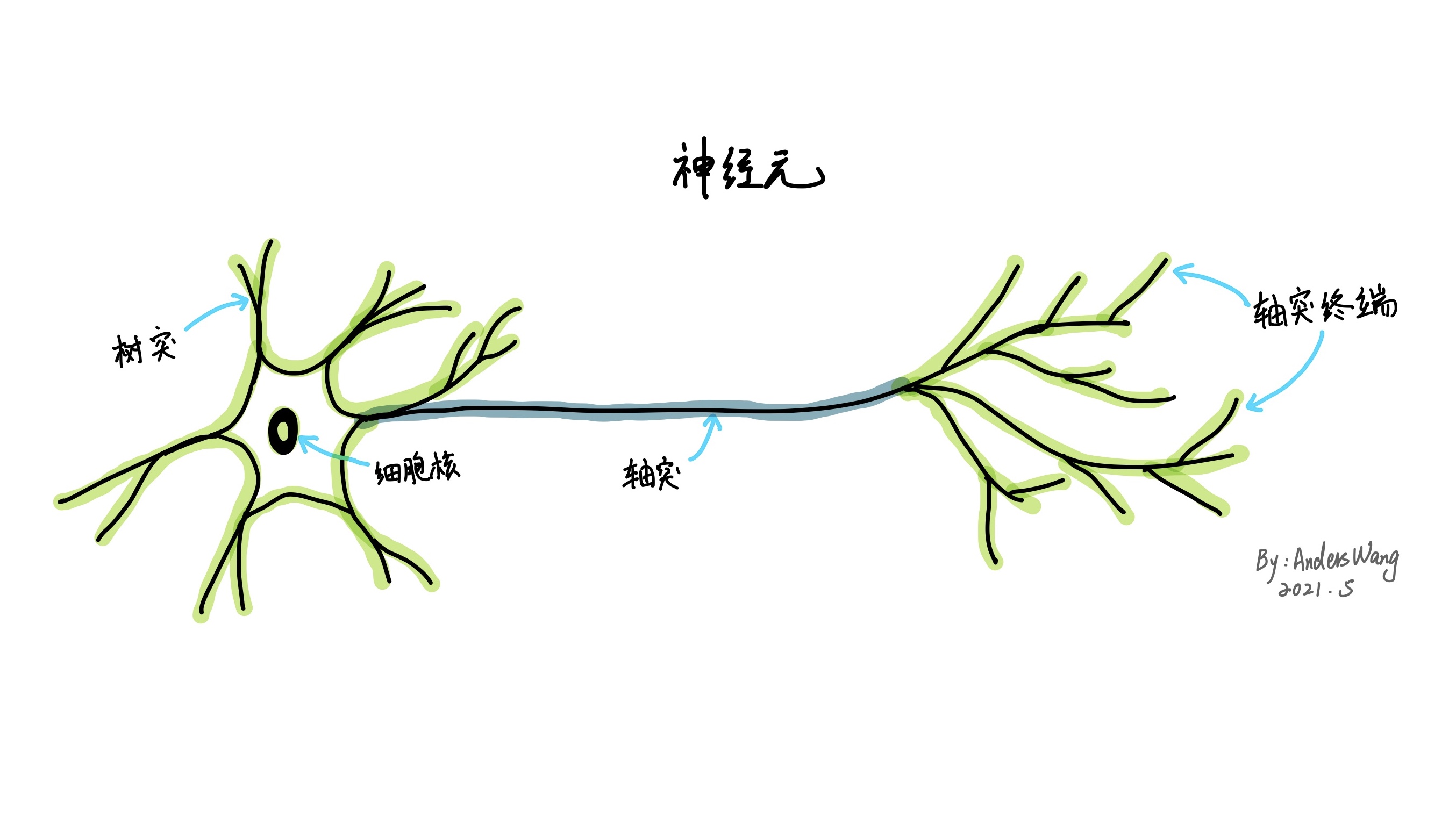
虽然神经元有各种形式，但是所有的神经元大致都是将电信号从一端传输到另一端，然后沿着轴突把信号从树突传到树突。最后这些信号从一个神经元传送到另一个神经元。比方说我们的身体可以感知光、触感，声音等信号，就是来自感官神经元的信号最终传到了我们的大脑，而大脑也是由各种神经元组成的。

而人工神经网络是在理解和抽象了人脑结构及其对外界刺激的响应机制后，以生物神经系统的基本原理和结构为范本原型，以网络拓扑为理论基础，对复杂信息进行非线性关系表示和逻辑操作的一种数学模型。这里要说明的是并没有任何科学证明神经网络就是人脑结构的翻版，只能说是借鉴于人们对人脑结构的了解而启发创造的一种人工神经网络模型。

2、人工神经网络大致流程

手写数字识别被称为神经网络领域的 "Hello World"，因为识别人手写笔记的这个问题是检验人工智能基本的理想挑战，要让计算机准确区分图像中包含的内容。所以我把对MNIST的图像识别视为进入人工神经网络的大门。

在开始讲解代码实现神经网络之前，让我们先梳理一下神经网络流程的大致过程。首先，数据集是构建算法模型最重要的起点。如下图所示整个人工神经网络的过程大致可以分为这几步，导入数据集，并且对数据集进行必要的转换以此达到符合模型所需的矩阵数据格式；接着用划分的训练集对神经网络模型进行训练，当模型的准确度训练到一定程度后，最终就能通过训练好的神经网络模型进行图像识别查验了。

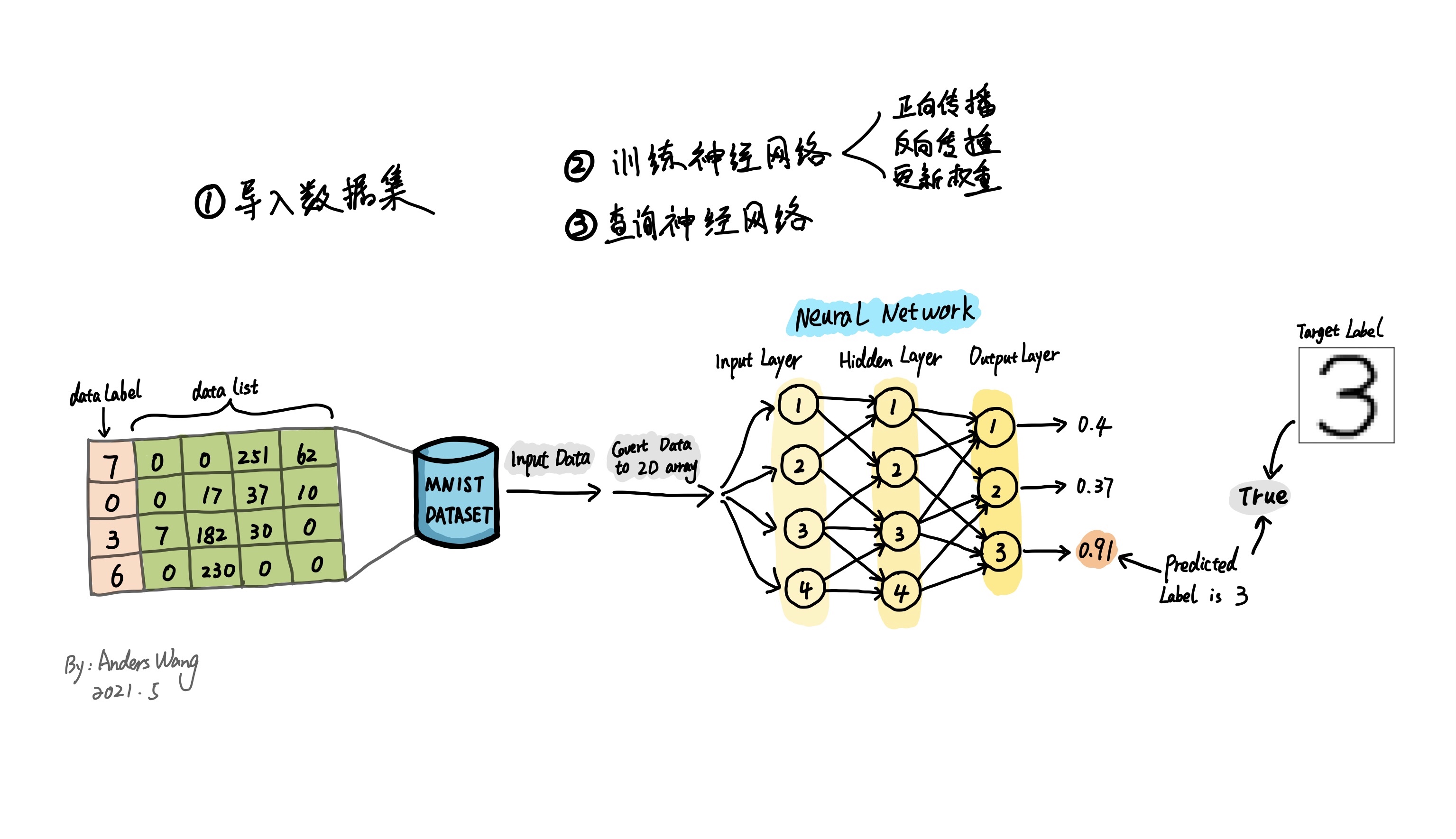
3、准备MNIST数据集

MNIST 数据集是著名的手写图像集合，常用来测量和比较机器学习算法的性能。该数据集包括了用于训练机器学习模型的 60,000 个图像和用于测试性能的 10,000 个图像。现成的MNIST的数据集主要是CSV文件，它的格式如下图分解图所示。每一行由一连串数字分别以逗号隔开。其中第一个值是数据标签，代表图像的实际"数字"，比如第一个值为 2那这个图像应该被识别为 2。随后的一连串数值由逗号分隔代表手写数字的组成像素值，由于像素的尺寸是28*28=784，所以除去首位标签值后，还有一共784个值。

4、神经网络的运行基本原理

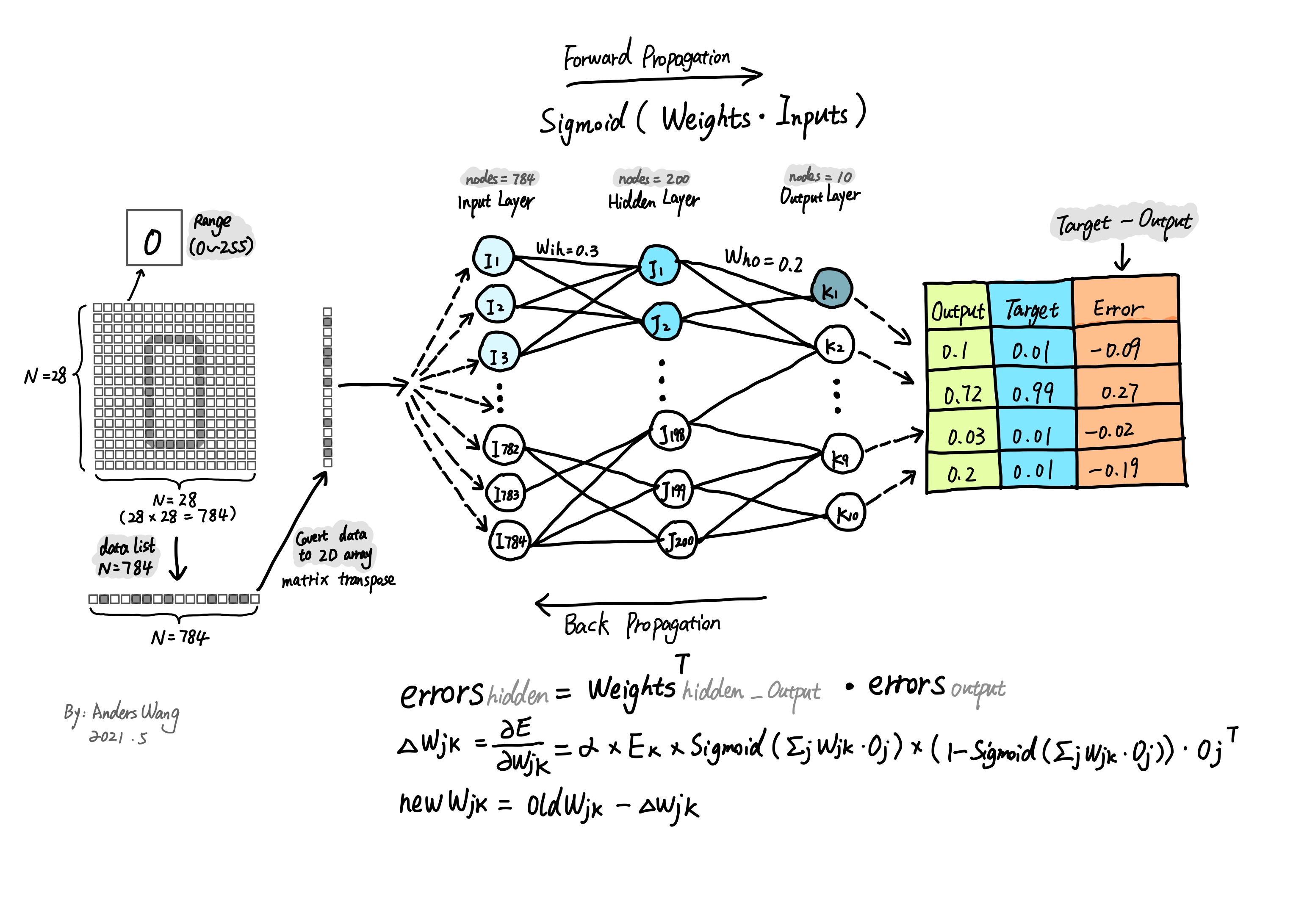
如之前开头所说的那样，神经网络的运行过程大致可以分为接收导入的数据，然后进行训练，最后用输出结果误差对过程中的链接权重进行更新，最后生成模型。这中间训练的过程尤为重要，如下图所示我们的数据集是由784个数值组成的，这784个数值作为第一层输入层被分为了784个输入层节点，经过与下一层的链接权重进行一系列的组合计算并应用激活函数后完成第一遍输出值。接着通过这个输出值与目标值的比较得到误差值，最后使用误差值反向更新权重以此来调节链接权重的大小，反复几次操作后神经网络模型生成完毕。

4.1、神经网络的计算过程 --- 信号正向传播

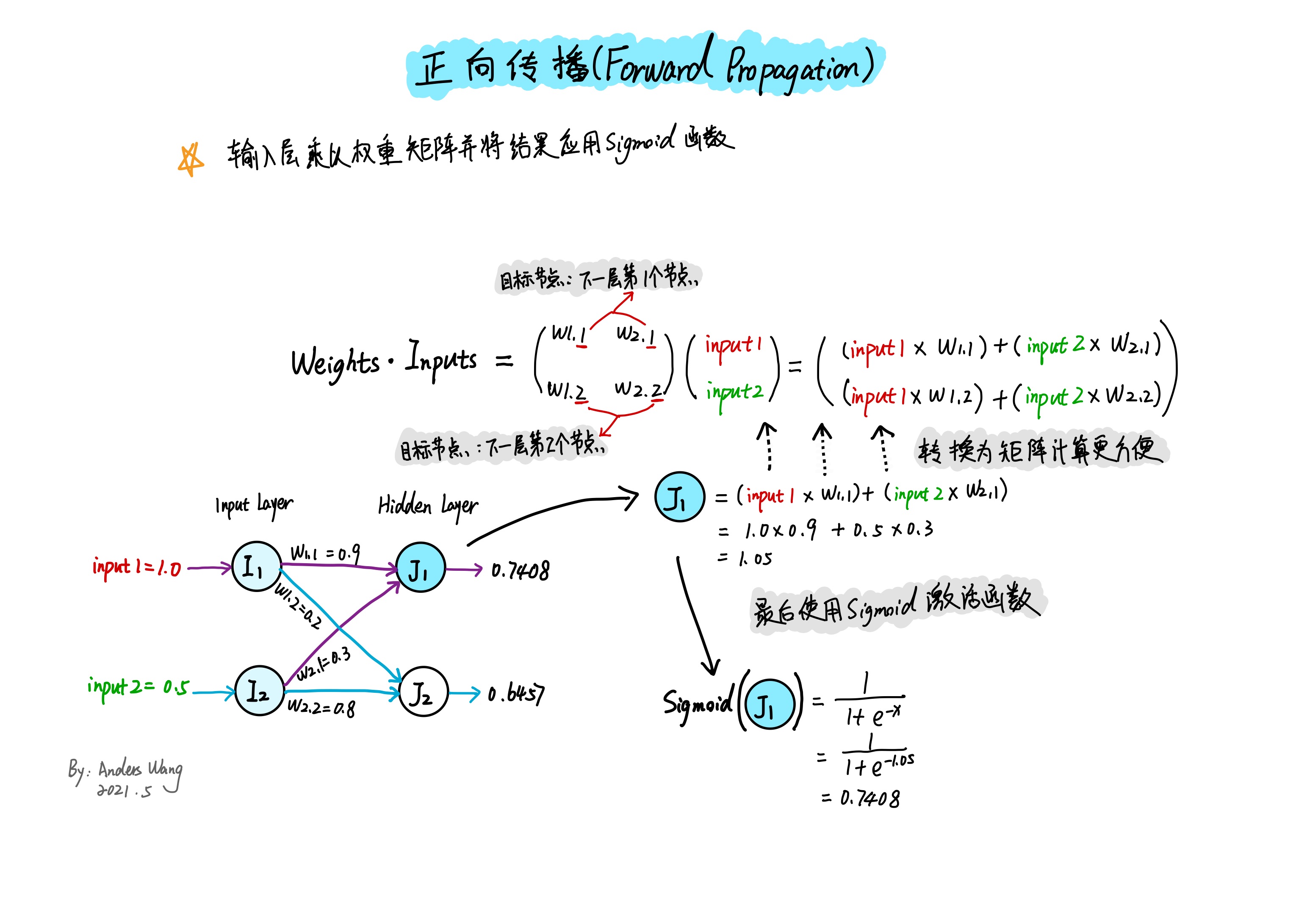
神经网络信号的传播是由输入到最终输出的过程，输入的数值经过 输入层 到 隐藏层 之间的链接权重进行组合计算，最后应用激活函数来调节输出信号值。这样依次从输入层到最终输出层计算的过程称为信号的正向传播。

如上图所示为了更好的说明，以求得隐藏层第一个节点$J_ {1}$为例，首先在求任何层的节点数值时需要通过上一层（即输入层）的输入数值与对应的链接权重相乘来获得对应的隐藏层节点数值，这是一个组合计算的过程。可以发现隐藏层 $J_ {1}$ 节点的数值是由输入层 $I_ {1}$ 和 $I_ {2}$ 两个节点组成，所以分别将输入数值乘以与目标节点对应的链接权重：$I_ {1} \times W_ {1,1} + I_ {2} \times W_ {2,1}=J_ {1}$ 求得隐藏层 $J_ {1}$ 节点的数值，之后必须将数值应用于Sigmoid激活函数来调节输入信号。

想要求得更多的隐藏层节点输入信号就需要更多的输入层数值乘以对应链接权重，并最后应用激活函数求得，但是用这样的书写来计算所有节点过于麻烦，最方便的办法就是使用矩阵。通过上图可以发现，其实可以使用矩阵乘法表示所有组合计算，$X = {W}\cdot{I}$，这里$X$ 是输出矩阵， $W$ 是权重矩阵，$I$ 是输入矩阵。所以正向传播求得每一层节点输出值的过程就是 $Sigmoid(X) = {W}\cdot{I}$。

4.2、神经网络的计算过程 --- 误差反向向传播

正向传播的计算过程我们已经明白了，但是这样来判断一个结果来说还是远远不够的。因为所有传入的数据仅仅是通过组合计算在神经网络层上进行了一次正向传播而已，正由于初始的链接权重通常是随机值，基于这样的组合计算得到的输出值必然与目标值会有很大的误差，因此还需要通过这个误差值反向对链接权重进行优化（如误差过大，就调小权重，反之增大），这样做的目的是为了神经网络经过层层计算后得到的输出值更接近实际目标值。

为了更清晰描述反向传播过程，我将它分解成为两个细节部分，第一部分求得前一层（即隐藏层）误差的过程，第二部分为借助这个误差来更新权重的过程。

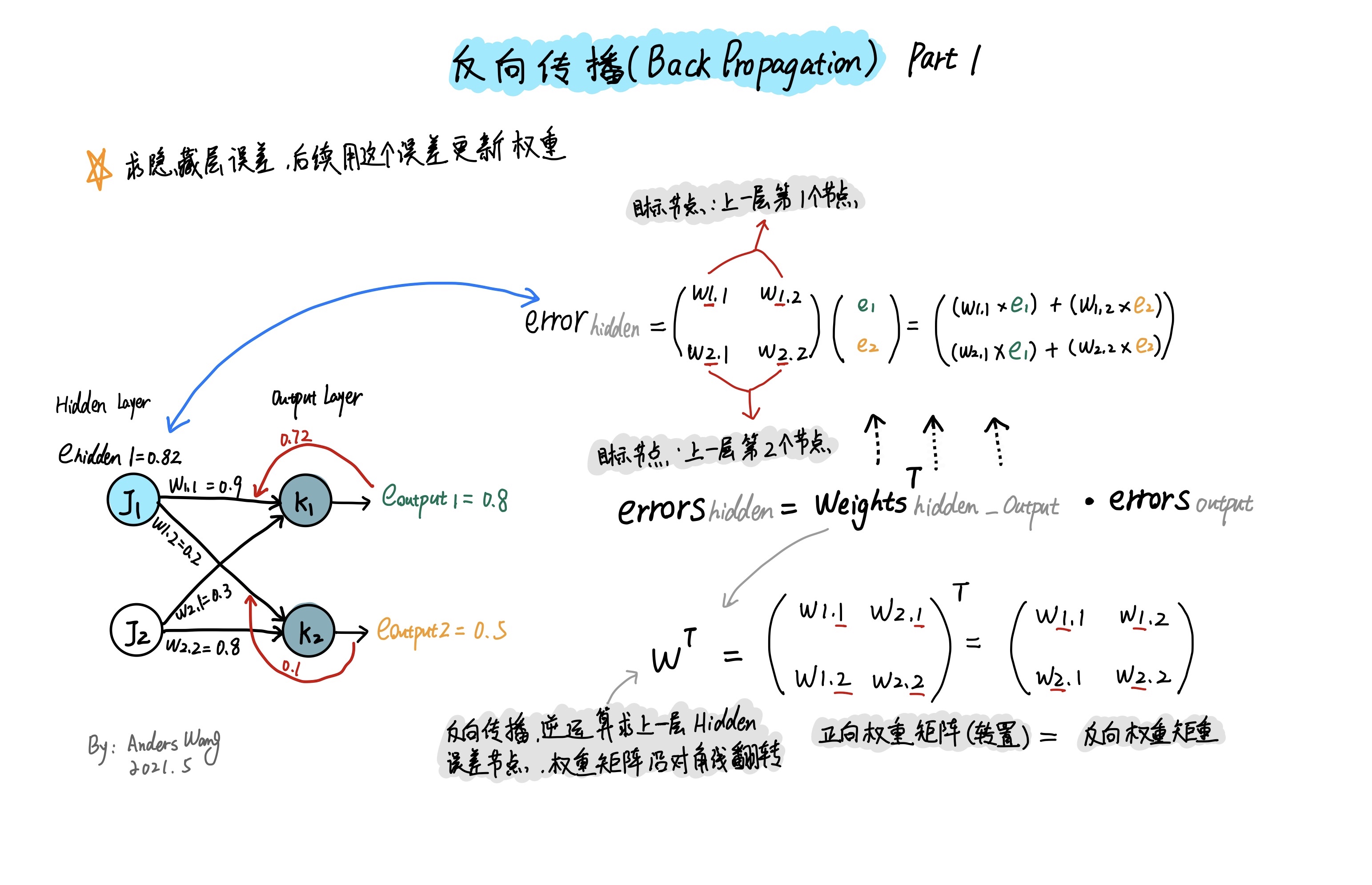
神经网络在进行反向传播前必然进行了一次正向传播，在正向传播的过程中经过输出层后会得到输出层的输出值，而通过目标值与这个输出值相减就可以得到输出层的实际误差值。而这个误差值还可以反向得到上一层（隐藏层）的误差值。你或许会问为什么还要计算出隐藏层的误差呢，因为我们需要使用隐藏的误差值来更新隐藏层到输出层之间的权重值。

但是反向计算上一层的误差值的方法可以有很多种，大致可以分为如下4种。

（1）直接将误差值以链接权重的个数N来平分，如输出层的误差值是由2个链接对应的节点组成，所以就以$\frac{1}{2}$分割误差值：

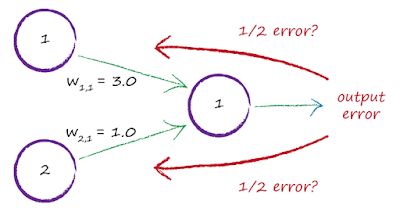
（2）采用以链接权重值的占比来计算：

这种方法的思想是不同的链接权重具有不同的权重强度，所以理应以权重值大小的比例来分割误差值。如下图$W_ {1,1}$的权重值为3.0，$W_ {2,1}$的权重值为1.0，那么$W_ {1,1}$的权重强度比重为$\frac{W_ {1,1}}{W_ {1,1}+W_ {2,1}}=\frac{3}{4}$，$W_ {2,1}$的权重强度比重为$\frac{W_ {2,1}}{W_ {1,1} + W_ {2,1}}=\frac{1}{4}$，也就是说上一层的节点$1$将获得$\frac{3}{4}$比例的误差值，而节点$2$将获得$\frac{1}{4}$比例的误差值，使用这种方式的好处是后续能更精确的优化权重数值，但是这也有个缺点，就是我们很难通过这种方式去进行大量的计算，即使使用了矩阵计算。

（3）直接用误差与链接权重相乘 $E_ {hidden}=W_ {i,j}^T⋅E_ {output}$（这也是本文使用的方法）。

以上图为例，反向计算 $(E)J_ {1} 节点的误差值是由 W_ {1,1} 和 W_ {1,2}$ 链接权重组成，所以计算该节点的过程就是$(E)J_ {1}=(E)K_ {1} \times W_ {1,1} + (E)K_ {2} \times W_ {1,2}$ 这种方法的好处是计算非常简单，即使反馈的误差值过大或过小，但在下一轮的迭代中，神经网路也可以自行纠正。

注意，由于是反向计算，链接权重排列的顺序与之前正向传播时的顺序不同，所以这里需要对链接权重的矩阵进行转置。

（4）与第3种方式相近，但是表达式额外除以了对应的链接权重个数N：

$E_ {hidden}=\frac{W_ {i,j}^T}{N}.E_ {output}$

这样做的方式有点类似某种形式的归一化，对于某些过大或者过小误差来说，可以缩小一定误差的比例范围。

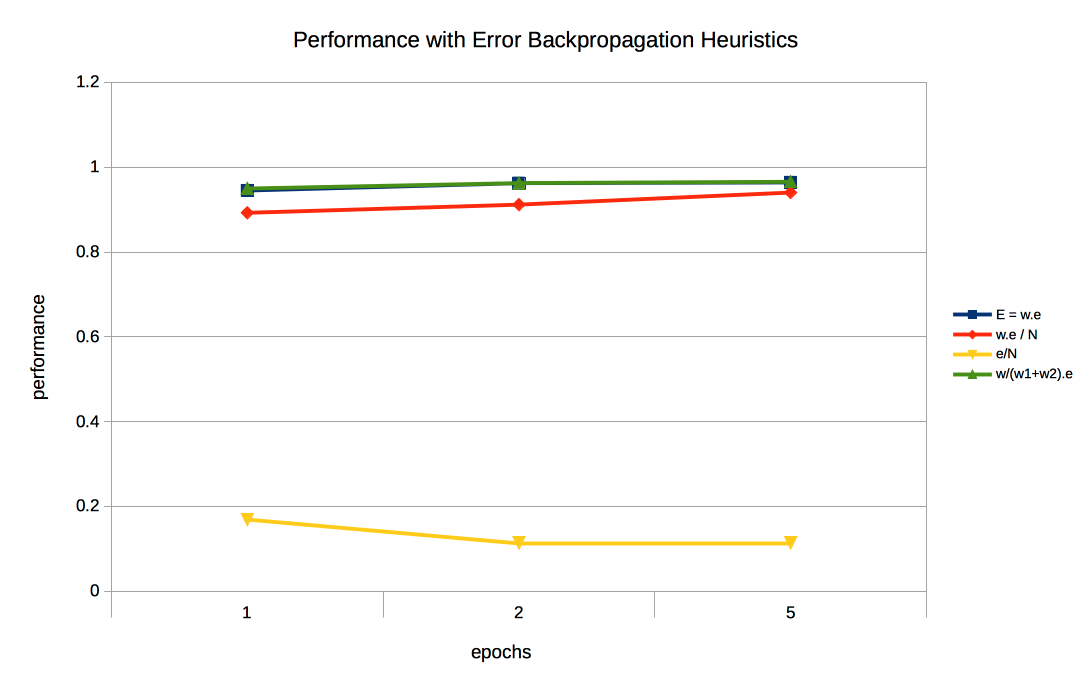
为了更好的说明这四种方法实际计算的效果如何，如下统计图是对不同方式的性能计算展示。蓝色代表（第3种）使用权重值与输出层误差值直接相乘，红色代表（第4种）仅仅增加归一化的形式，黄色代表（第1种）直接将误差值以链接权重的个数N来均匀分割，绿色代表（第2种）以链接权重值的实际占比计算。

最后可以发现蓝色和绿色线形图在多次循环训练后都得到了不错的结果。而出于易于计算的考虑，最终选择直接将输出层的误差值与链接权重值相乘的这种方式来计算隐藏层的误差值。

这里不得不提到的一点是，当神经网络多于2层时，那么只需从最终输出层往回工作，重复应用相同的思路计算出前一层的误差值就可以了。

在获得了上一层（隐藏层）的误差值后，就可以真正的通过误差来调整对应的链接权重了。为了希望得到最小化的误差函数，我们试图要知道误差对链接权重的改变有多敏感，换个方式说就是当权重$W_ {ij}$ 这个自变量变化时，误差$E$这个因变量是如何改变的，所以我们需要做的是对链接权重求导，就是$\frac{\partial{E}}{\partial{W_ {jk}}}$ 。

如上求导的过程中使用了链式法则，而在链式法则的计算中需要代入前一层（隐藏层）的误差值，这也再次证明了我们为什么之前反复提到需要求得前一层的误差值是必须的了。通过推导可以得到如下两个链接权重的更新公式：

隐藏层与输出层的权重变化率： $\Delta{W_ {jk}}=-E_ {k}\times{Sigmoid(O_ {k})\times(1-Sigmoid(O_ {k}))\cdot{O^T_ {j}}}$

输入层与隐藏层的权重变化率： $\Delta{W_ {ij}}=-E_ {j}\times{Sigmoid(O_ {j})\times(1-Sigmoid(O_ {j}))\cdot{O^T_ {i}}}$

最后我们只需要把旧权重与新权重进行相减来更新权重：

$newW_ {jk}=oldW_ {jk}-\Delta{W_ {jk}}$

由于直接选择合适的权重太难了，另一种方法是通过误差函数的梯度下降来采取小步长，迭代的改进权重，也就是所谓的梯度下降法，为了使每次调整斜率以合适的步长幅度调整，可以引入learning rate学习率的概念，所以最终的公式可以演变为：

$newW_ {jk}=oldW_ {jk}+\alpha\times\Delta{W_ {jk}}$

至此这就是对于神经网络如何训练并自我更新权重的所有计算过程。

Python代码实现

接下来就是纯Python实现人工神经网络的所有代码，先导入最基本的模块库，这里除了最基本的numpy和pandas外，还因为后面需要更好的呈现识别图像的结果，所以还用到了matplotlib。另外由于要进行大量的数学运算所以不得不借助scipy这个科学计算包。由于神经网络训练是一个随机的过程，有时候工作的不错，有时候就很糟糕，所以为了更好的每次测试比对，这里设置了随机种子以保证每次的随机影响能保持一致。

import numpy as np  
import pandas as pd  
import matplotlib.pyplot as plt  
import scipy.special

from scipy import stats

np.random.seed(80)  

神经网络的整个结构其实很简单，如下代码由一个名为NeuralNetwork的类以及内部几个主要方法构成。主要包含3大方法：

_init_()方法：定义神经网络的基本参数，其中分别设置了输入层、隐藏层、输出层的节点数参数，以及输入层与隐藏层的权重值、隐藏层与输出层的权重值、学习率、激活函数。

train()方法：由于神经网络的训练模式组成是先通过正向传播得到基本误差，然后反向传播使用误差更新权重。所以在该方法里分别要实现正反向传播操作的过程。

query()方法：经过之前的一系列训练后，神经网络的连接权重值都已经优化到最佳数值，所以对于查询方法，只需要传入数据集进行一遍正向传播就可以输出结果。

### neural network class definition ###
class NeuralNetwork:  
    ### initialise the neural network elements
    def __init__(self, input_nodes, hidden_nodes, output_nodes, learning_rate):
        self.i_nodes = input_nodes
        self.h_nodes = hidden_nodes
        self.o_nodes = output_nodes
        self.lr = learning_rate

        self.wih = np.random.normal(0.0, pow(self.h_nodes, -0.5), (self.h_nodes, self.i_nodes))
        self.who = np.random.normal(0.0, pow(self.o_nodes, -0.5), (self.o_nodes, self.h_nodes))

        # activation function is the sigmoid function
        self.activation_function = lambda x: scipy.special.expit(x)


    ### training the neural network
    def train(self, inputs_list, targets_list):
        # convert the list to 2d array, because the each layer of data format must be 2D
        inputs = np.array(inputs_list, ndmin = 2).T
        targets = np.array(targets_list, ndmin = 2).T

        # calculate the signals into hidden layer
        hidden_inputs = np.dot(self.wih, inputs)
        # calculate the signals emerging from hidden layer
        hidden_outputs = self.activation_function(hidden_inputs)

        # calculate the signals into output layer
        final_inputs = np.dot(self.who, hidden_outputs)
        # calculate the signals emerging from final layer
        final_outputs = self.activation_function(final_inputs)

        # error is the (target - actual): 
        output_errors = targets - final_outputs

        # hidden layer error is the output_errors, split by weights, recombined at hidden nodes
        hidden_errors = np.dot(self.who.T, output_errors)

        # update the weights for the links between the hidden and output layers
        self.who += self.lr * np.dot((output_errors * final_outputs * (1.0 - final_outputs)), np.transpose(hidden_outputs))
        # update the weights for the links between the hidden and input layers
        self.wih += self.lr * np.dot((hidden_errors * hidden_outputs * (1.0 - hidden_outputs)), np.transpose(inputs))


    ### query the neural network
    def query(self, inputs_list):
        # covert inputs list to 2d array
        inputs = np.array(inputs_list, ndmin = 2).T

        # calculate signals into hidden layer
        hidden_inputs = np.dot(self.wih, inputs)
        # calculate signals emerging from hidden layer
        hidden_outputs = self.activation_function(hidden_inputs)

        # calculate signals into output layer
        final_inputs = np.dot(self.who, hidden_outputs)
        # calculate signals emerging from output layer
        final_outputs = self.activation_function(final_inputs)

        return final_outputs

如下代码是先创建神经网络对象，并这个对象设置基本参数，由于我们之前已经提到一个数字有784个像素数值构成，所以初始的输入节点自然为784个，而隐藏层的节点数通过一系列调参观察后，这里设置为200比较合适，而最后的输出数值设置为10的原因是因为我们要识别的阿拉伯数字为0~9十个数字，结果必然是10个节点中的某一个，最后的学习率设置为0.1也是通过调参观察而定的。最后设置了5个世代作为循环次数，是因为经过几次实验后发现使用5个世代循环训练在当前的过程中效果更佳，如果再增加下去就会出现过拟合的情况。

不得不提到的一点是由于数据的有限性，所以在已有数据的基础上代码最后还使用了rotate逆时针顺时针旋转的方式，以使现有数据产生变种来增加数据量，这样可以为模型增加训练强度。

### training the neural network ###
# loading the mnist traning data CSV file into list
training_data_file = open("neuralnetwork/mnist_dataset/mnist_train.csv", 'r')  
training_data_list = training_data_file.readlines()  
training_data_file.close()

# define the number of input, hidden, output nodes and learning rate
input_nodes = 784  
hidden_nodes = 200  
output_nodes = 10  
learning_rate = 0.1

# create the instance of neural network
n = NeuralNetwork(input_nodes, hidden_nodes, output_nodes, learning_rate)

# epochs is the number of times the training data set is used for training
epochs = 5

for e in range(epochs):  
    # go through all records in the traning data set
    for record in training_data_list:
        # split the record by the ',' commas
        all_values = record.split(',')

        # scale and shift the inputs
        inputs = (np.array(all_values[1:], dtype = np.float) / 255.0 * 0.99) + 0.01

        # create the target output values(because we use the sigmoid function, 
        # its range is 0<s<1, all 0.01, expect the desired label which is 0.99)
        targets = np.zeros(output_nodes) + 0.01

        # all_values[0] is the target label for this record
        targets[int(all_values[0])] = 0.99
        # training the model
        n.train(inputs, targets)

        ## create rotated variations in order to increase the sample capacity
        # rotated anticlockwise by x degrees
        inputs_plusx_img = scipy.ndimage.interpolation.rotate(inputs.reshape(28,28), 10, cval=0.01, order=1, reshape=False)
        # training the model
        n.train(inputs_plusx_img.reshape(784), targets)

        # rotated clockwise by x degrees
        inputs_minusx_img = scipy.ndimage.interpolation.rotate(inputs.reshape(28,28), -10, cval=0.01, order=1, reshape=False)
        # training the model
        n.train(inputs_minusx_img.reshape(784), targets)      

接下来使用测试集对神经网络模型进行测试并评分。

### test the neural network ###
# load the test data
test_data_file = open("neuralnetwork/mnist_dataset/mnist_test.csv", "r")  
test_data_list = test_data_file.readlines()  
test_data_file.close()


# scorecard for how well the network performs, initially empty
scorecard = []

# go through all the records in the test data set
for record in test_data_list:  
    # split the record by the ',' commas
    all_values = record.split(',')

    # convert answer is first label
    correct_label = int(all_values[0])

    inputs = (np.array(all_values[1:], dtype = np.float) / 255.0 * 0.99) + 0.01

    ## query the neural network
    outputs = n.query(inputs)

    # the index of the highest value corrsponds to the label
    predict_label = np.argmax(outputs)

    if (predict_label == correct_label):
        scorecard.append(1)
    else:
        scorecard.append(0)

# calculate the performance score, the fraction of correct answers
scorecard_array = np.array(scorecard)  
print(f'performance: {round(scorecard_array.sum() / scorecard_array.size * 100, 2)}%')  

测试评分结果为96.65%的正确率，这个结果还是十分不错的。

performance: 96.65%  

最后为了更好的展现，我对模型进行批量输入并进行可视化展示，一起来看看实际效果如何。

### test the custom image ###
from pathlib2 import Path  
import imageio  
import matplotlib.pyplot as plt


img_array_list = []

files_path = Path.cwd().joinpath('neuralnetwork/my_own_images')  
if files_path.exists():  
    for file in files_path.iterdir():
        if file.match('*.png'):
            img_array = imageio.imread(str(file), as_gray = True)
            img_array_list.append(255.0 - img_array)

fig, axes = plt.subplots(figsize=(6, 6), nrows = 3, ncols = 3)  
i = 0

for row in range(3):  
    for col in range(3):
        # reshape the 784 based on white ground
        img_data = img_array_list[i].reshape(784)
        # scale and shift the inputs
        inputs = (img_data / 255.0 * 0.99) + 0.01
        # query the neural network
        outputs = n.query(inputs)

        # the index of the highest value corresponds to the target label
        label = np.argmax(outputs)

        axes[row][col].imshow(img_array_list[i], cmap = 'Greys', interpolation = 'None')
        axes[row][col].set_title(f'predict:{label}')
        axes[row][col].set_xticks([])
        axes[row][col].set_yticks([])

        i += 1

如下图所示，从图示结果看预测成功率还不错，除了把6错误的预测为9外，其它均预测正确。我猜可能是由于背景有色差噪点的关系导致没有正确识别，加上先前训练模型的样本中可能也不存在这样的情况。

之前提到，带有噪声的数字6没有被正确识别，可能是由于训练模型时不存在类似的样本作为训练数据，所以导致判断错误。为了验证这点，我干脆把这个未识别的图像作为训练集单独拎出来再次训练下模型，看看模型最终能不能识别正确。

将未识别正确的数据作为样本训练了10次后，果真最后可以将带有噪声的数字6识别正确了。当然这种方式属于拿测试集当训练集的作弊行为了。